Spacecraft Motion Under Gravity and Aerodynamic Torque Bhardwaj Rashmi1,*, Sethi Mani1 1Department of Mathematics, School of Basic and Applied Sciences Guru Gobind Singh Indraprastha University, Kashmere Gate, Delhi-110 006, India *Author for Correspondence, E-mail: rashmi@ipu.edu; rb_22@rediffmail.com
Abstract This paper deals with the study of the non-linear planar oscillation of a satellite in a circular orbit under the influence of aerodynamic torque. Throught Melnikov's method, we have discussed that the equations of motion are non-integrable. The non-integrability in Earth-Satellite system has also been discussed graphically. Top AMS Subject Classification 70M, 74G25. Top Keywords Aerodynamic torque, Air drag, Non-linear, Planar oscillation. Top |
Introduction The interaction of the upper atmosphere with a satellite's surface produces a torque about the latter's centre of mass. For spacecraft below approximately 400 km. the aerodynamic torque is the dominant environmental disturbance torque. This aerodynamic torque increases as the spacecraft altitude decreases. Any spacecraft in orbit is under the action of several kinds of external disturbance torques. The dynamics of rotating bodies has been studied by Inarrea and Lanchares [1] under the influence of aerodynamic drag. Kauprianov and Shevchenko [2] have studied the problem of observability of chaotic regimes in the rotation of planetary satellites. El-Salam et al. [3] constructed a second order atmospheric drag theory based on the usage of TD88 model. macicjewski and Przybylska [4] analysed the integrability of a dynamical system under the influence of gravitational and magnetic fields. Markeev and Bardin [5] used the kAM theory to study the orbital stability of planar oscillation and satellite rotations. Peng and Liu [6] have considered free gyrostats with a slightly asymmetric rotor. A quantitative description of Hamiltonian chaos based on Riemannian geometrisation of Newtonian dynamics has been discussed by Ciraolo and Pettini [7]. This paper studies the effect of gravity and aerodynamic torque on spacecraft motion. |
Top Equation of Motion Consider a rigid satellite S moving around the Earth E in a circular orbit such that the orbital plane coincides with the equatorial plane of the Earth (Fig. 1). The body is assumed to be tri-axial body with principal moments of inertia A < B < C at its centre of mass. C is the moment of inertia about the spin axis, which is perpendicular to the orbital plane. These principal axes are taken as the coordinate axes x, y, z; the z-axis being perpendicular to the orbital plane. Let r̅ be the instantaneous radius vector of the centre of mass of the satellite, θ the angle that the long axis of the satellite make with a fixed line EF lying in the orbital plane and δ/2 the angle between the radius vector r̅ and the long axis. |
Eule's dynamical equation of motion about the z-axis is given by |
where GZ = z –component of the gravitational torque 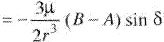 |
μ= G(mE + ms) ≅ GmE = Gravitational constant |
ms = Mass of the Satellite |
NZ = z –component of aerodynamic torque and ω1, ω2, ω3 are angular velocities about the principal axes at the center of mass of the satellite. |
where ρ is the atmospheric density. S the effective surface normal to the velocity vector. Cd the drag coefficient of the body,  the velocity of the satellite relative to the atmosphere [8] the velocity of the satellite relative to the atmosphere [8] |
Taking α (true anomaly as an independent variable). the equation of motion is |
Hamilton's Equation Equation (2) is equivalent to the Hamilton's equations where H is the Hamiltonian function. H can be written as H = H0 + εH1 +… In this problem where Equilibrium and Double Asymptotic Solution The equilibrium solution corresponding to H0 is given by which gives us q(α) = 0, π, p(α) = 0. Thus in the phase space, (0, 0) and (π, 0) are the equilibrium points, (0, 0) is a stable conjugate point and (π, 0) is an unstable conjugate point. Also, the unperturbed double asymptotic solutions at (π, 0) are obtained as Top Melnikov's Function The Melnikov's integral [9] is defined as |
Graphical Representation of Melnikov's Function We have studied the graphical representation of Melnikov's function in Earth-satellite system. Figure 2 illustrates the graph of M± (ν0, b, n, d) for 0 ≤ n ≤ 1. In all these cases, the caese, it is observed that initially, the curves increase/decrease very slowly and, thereafter, exponentially increase/decreases to ± ∞ as mass distribution parameter n of satellite changes. Figure 3 illustrates the graph of M± (ν0, b, n, d) for 0 ≤ ν0 ≤ 10, In all these cases, the Melnikov's function M± (ν0) behaves almost like sine functions, one corresponding to M+ (ν0) and the other for M– (ν0). Loops elongate along the ordinate and they have simple zeros. Figure 4 illustrates the graph of M± (ν0, b, n, d) for 0 ≤ b ≤ 1. In all these cases, it is observed that as the parameter due to air drag effect b changes from 0 to 1. the Melnikov's function M+(b) and M–(b) almost remain constant. Figure 5 illustrates the graph of M± (ν0, b, n, d) for 0 ≤ d ≤ 1. In all these cases, it is observed that as d changes from 0 to 1, the Melnikov's function M+(d) and M–(d) almost remain constant and expand along the ordinate. Top Conclusion The non-linear planar oscillation of a satellite under the influence of air drag has been studied. It was observed that (0, 0) and (π, 0) behave as stable and unstable equilibrium points, respectively. By using Melnikov's method, it has been concluded that the non-linear rotational equations of motion of the planar oscillation of a satellite in circular orbit under the influence of aerodynamic torque are non-integrable. Graphically, in the Earth-satellite system, Melnikov's function has simple zeros that change with mass distribution parameter n and, hence, equation of motion are non-integrable. |
Top Figures |